Implied Volatility (IV)
Implied Volatility of a stock or an index is computed using an option pricing model such as the Black-Scholes. In contrast to historical volatility, which is a measure of price changes in the past, Implied Volatility reflects expectations regarding the stock or market's future volatility. It can also help to gauge whether options are cheap or expensive. Rising implied volatility causes option prices to rise or become more expensive; falling implied volatility results in lower option premiums. Therefore, with everything else being equal, when implied volatility on an option is high, it is better to sell that option; If the implied volatility is low, the option more suitable for buying.
To solve for implied volatility, option pricing models require:
- the option's expiration date
- the strike price of the option
- the price of the underlying asset
- the dividends paid
- the prevailing interest rate
- the current option's price
- style of options
- call/put
As mentioned above, when the option premium increases but the other factors remain the same, the change in option price is due to a change in implied volatility. Each option contract has a unique level of implied volatility, which can change over time and as the demand for an option rises or falls. To determine at any given point of time whether implied volatility is relatively high or low (i.e. whether an option is relatively cheap or expensive) it is important to compare the current value of volatility to the levels that existed in the past.
The Black-Scholes model suggests that every option imply the same volatility for underlying, but as it can be seen from practice every option implies different volatility. Implied volatility often tends to be higher for out-the-money (OTM) and in-the-money (ITM) options compared to at-the-money, in this case OTM and ITM options represent increased risk on potentially very large movements in the underlying; to compensate for this risk, they tend to be priced higher. Sometimes Implied Volatility for OTM and ITM options is lower than for ATM. For more information see Volatility Skew.
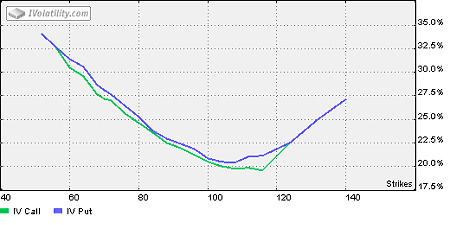
As mentioned above, each option contract has a unique level of volatility. It is referred to as a skew of implied volatility. Large skew creates trading opportunities. Implied Volatility can be used to monitor the market's opinion about the Volatility of a particular stock, to estimate the price of one option from the price of another option. As implied volatilities are different for different options, it is better to use some representative value of volatility for analysis, for example, the Implied Volatility Index, Normalized Volatility Surface, VIX etc
One of the convenient ways of looking at the volatilities of all options in a historical perspective is the volatility surface, which is described below.