Kurtosis
Excess Kurtosis is the relative peakedness or flatness of a returns distribution compared to the normal distribution (a normal distribution has a zero excess kurtosis). A distribution is said to be leptokurtic if its tails are fatter than those of a corresponding normal distribution. It is said to be platykurtic if its tails are thinner than those of the normal distribution. Market returns for stocks tend to be slightly leptokurtic. This means that dramatic market moves occur with greater frequency than is predicted by the normal distribution.
\( E_k = \frac{n * (n + 1)}{(n - 1) * (n - 2) * (n - 3)} \frac{\frac{\sum_1^{n} (X - \bar{X})^{4}}{n - 1}}{\lbrack \frac{\sum_1^{n} (X - \bar{X})^{2}}{n - 1} \rbrack^{4}} - \frac{3 * (n - 1)^{2}}{(n - 2) * (n - 3)} \)
Because excess kurtosis characterizes the flatness of returns, it can be applied to an option model. Consequently, a excess kurtosis greater than zero means fatter tails and the model underprices both out-of-the-money and in-the-money calls and puts. A excess kurtosis less than zero means thinner tails; and as a result, options are overpriced.
Terms available: 10, 20, 30, 60, 90, 120, 150, 180 days
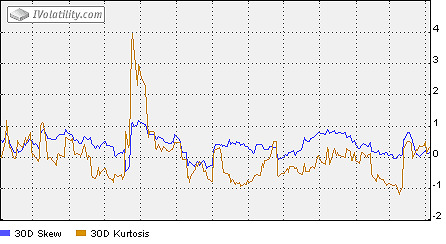
There are special options pricing models which use Skew and Excess Kurtosis as additional parameters.