Parkinson's Historical Volatility
The Parkinson number, or High Low Range Volatility, developed by the physicist, Michael Parkinson, in 1980 aims to estimate the Volatility of returns for a random walk using the high and low in any particular period. IVolatility.com calculates daily Parkinson values. Prices are observed on a fixed time interval. n=10, 20, 30, 60, 90, 120, 150, 180 days.
\(S_{H_t} \) is high stock's price in t day. \(S_{L_t} \) is low stock's price in t day.
High/Low Return ( xtHL ) is calculated as the natural logarithm of the ratio of a high stock's price to low stock's price. Return \( x^{HL}_t = \ln \frac{S_{H_t}}{S_{L_t}} \)
And Parkinson's number
\( HL_{HV_{daily}} = \sqrt{\frac{ \displaystyle\sum_{t=1}^{n} \frac{1}{4 * \ln 2} * \lparen x^{HL}_t \rparen^{2}} {n}} \)
An important use of the Parkinson number is the assessment of the distribution prices during the day as well as a better understanding of the market dynamics. Comparing the Parkinson number and periodically sampled volatility helps traders understand the tendency towards mean reversion in the market as well as the distribution of stop-losses.
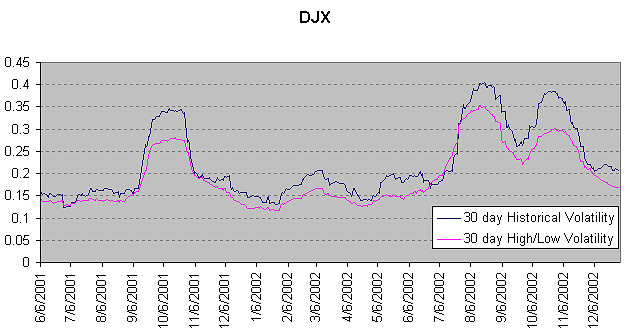
Currently, it is generally accepted that, at least to a good approximation, ln (S) follows a random walk. The diffusion constant of a random walk characterizes the variance.Instead of measuring using the traditional formula of Historical Volatility,we measure the difference between the maximum and minimum position during the same time interval. It is intuitively clear that this difference should be capable of giving a good estimation for the variance of returns.
Parkinson derived that the extreme value method is far superior to the traditional method and much more sensitive to variations of dispersion. The extreme value method is very easy to apply in practice since daily, weekly and monthly highs and lows are published for every stock. The advantage of using Parkinson Numbers to estimate Volatility can be of particular importance in studies of time and price dependence on Volatility as less data is needed to derive a given accuracy compared to the amount of data needed using the traditional method.