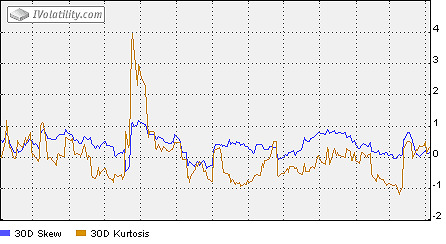
Skew
Skew is the degree of the asymmetry of a return's distribution around its mean. The commonly pictured "bell-shaped" or normal distribution is symmetric and has zero skewness. In positive skewness (a lognormal distribution has positive skewness), a large probability of a small loss is offset by a small probability of a large gain ("long shot"). In negative skewness, a small probability of a large loss is offset by a large probability of a small gain.
\( \displaystyle{A_1 = \frac{n}{(n - 1) * (n - 2)} \frac{\frac{\sum_1^{n} (X - \bar{X})^{3}}{n - 1}}{\lbrack \frac{\sum_1^{n} (X - \bar{X})^{2}}{n - 1} \rbrack^{3}}} \)
Applied to options trading it can be suggested that skewness indicates, along with Implied Volatility, how cheap or expensive options are at a given point in time. For example, a negative skew coefficient means that the density of a return''s distribution is asymmetric with a sharper fall on the right tail. Thus, put options are more expensive than call options.
Options models suggest that returns are normally distributed and underlying prices are lognormally distributed. Thus, the skew of a return's distribution is zero. Meaning up-and-down movement in theoretical models has the same probability.
Terms available: 10, 20, 30, 60, 90, 120, 150, 180 days