Historical Volatility (HV)
Historical Volatility reflects the past price movements of the underlying asset, while implied volatility is a measure of market expectations regarding the asset's future volatility. Historical volatility is also referred to as the asset's actual or realized volatility. There are different ways of measuring historical volatility. At www.ivolatility.com we use two of them.
The first kind of historical volatility, that is often called statistical volatility, is calculated as a standard deviation of a stock's returns over a fixed number of days. Return ( ) is defined as the natural logarithm of close-to-close prices. The section Price and Return's distribution demonstrates why using a logarithm of price relations is more convenient than using that of simple price relations. Standard deviation is a statistical measure of the variability of a set of numbers. Note, this volatility is a type of historical volatility, but not the only one. Nevertheless, when referring to historical volatility we will have in mind a standard deviation of stock's returns.
The other kind of historical volatility is High Low Range Volatility, or Parkinson's historical volatility, which is discussed below.
To calculate a standard deviation, closing stock prices ( ) are observed over different time frames. We
calculate standard deviation for the eight most popular terms: n=10, 20, 30, 60, 90, 120, 150, 180 days on a
daily basis. Thus historical volatility can be calculated by the following way.
Return \(x_t = \ln\left(\frac{P_t}{P_{t-1}}\right)\) where Pt is close price on day t.
\(\bar{X} = \frac{1}{n} \displaystyle\sum^{n}_{t=1} x_t\)
Daily historical volatility calculated on the basis of n days is estimated as
\(HV_{daily} = \sqrt{\frac{1}{n-1} \displaystyle\sum_{t=1}^{n} (x_t - \bar{x})^2} \)
Historical Volatility which is calculated as
\(HV = HV_{daily} * \sqrt{252} \) as we assume 252 traiding days in a year.
Note: In denominator we use n-1 instead of n to receive unbiased estimate of general dispersion (a square of a standard deviation). This adjustment is essential if we estimate standard deviation on the basis of a small number of observations.
Choosing an appropriate period of observation (n) is not easy. More data generally leads to more accuracy; however, Volatility does change over time and data from deep in the past may not be relevant for predicting the future. The best way for further evaluation is to use a term close to the period considered by most investors or traders.
Each index or stock has a unique level of volatility that changes over time. When historical volatility is high, it says that the stock has been showing extreme fluctuations in price. When it is low, it suggests quiet or sideways trading. Comparing it to the historical volatility of other stocks and indexes allows one to estimate whether the stock or index is relatively volatile.
Although volatility always changes, most indexes and stocks can be assigned an average value, since their volatility tends to fluctuate around some normal or average value over long periods of time. To determine what volatility level is normal for a particular stock or index, traders must consider historical volatility across different time frames. Furthermore, viewing the historical volatility of a stock or index over time can help to determine whether the volatility is rising or falling. For example, if the 10-day historical volatility of a stock is 15% and the 120-day is 45%, the stock has recently witnessed a sharp decline in volatility. Studying changes in the volatility of an asset can help identify a normal volatility range, deviations from it, and subsequently, trading opportunities.
Option premiums rise when market participants expect greater stock volatility. When the historical volatility of a stock or index is high, there is a tendency for the market to drive option premiums higher as well. One can expect a stock or index that has high historical volatility to exhibit high volatility in the future, and the option premiums will reflect those expectations.
Example
The table shows historical volatility for IBM calculated for different terms. As you can see 10-day historical volatility of 19.34% is relatively low, and 120-day historical volatility of 43.03% is relatively high. It means that a sharp decline in stock volatility occurred recently. Actually, as you can see on the volatility chart, 30 day historical volatility fell from 72% in October to 19.83% in March. The falling volatility was indirectly caused by a rising stock price, which began to lift in October after the company announced that it expected earnings to grow at more than 10 percent from the third quarter to the fourth quarter of 2002 due to an increase in market share.
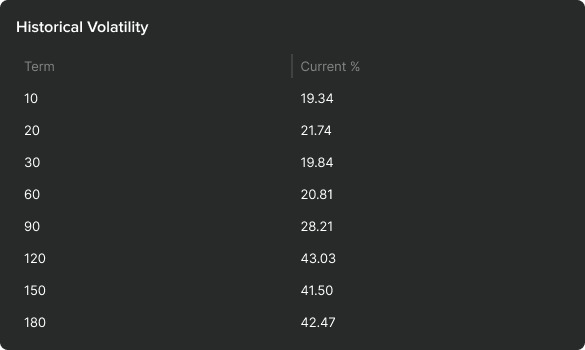
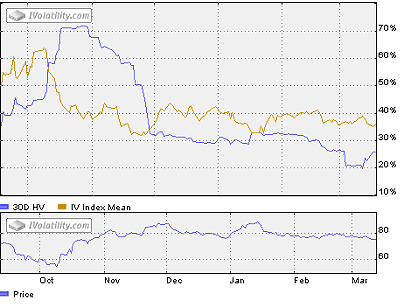 Chart: Historical Volatility, IV Index and price of IBM
Chart: Historical Volatility, IV Index and price of IBM
The Historical volatility vs HighHV and LowHV chart allows for comparison of the current historical volatility value (for different terms) with historical maximum and minimum values (for the last year). The vertical axis shows a scale representing the volatility value in %. The horizontal axis records the term.
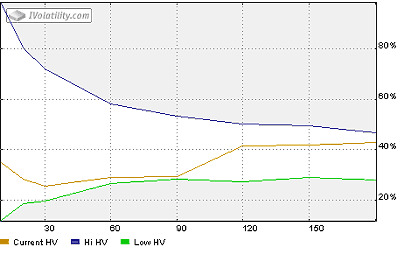 Chart: Current HV vs High and Low HV of IBM
Chart: Current HV vs High and Low HV of IBM