Correlation and Beta
Correlation and Betas are important values in stock and option analysis as they provide an idea as to how risky an underlying is in comparison with market.
Correlation between two stock/indexes returns (close-to-close prices) is a measure of how closely two equities' returns move together.
Beta of one stock against other is the linear coefficient between two equity's returns ( ). Beta of a stock against market index shows dependence between asset's return and market return, and it is a measure of the systematic risk, or the market risk, of the asset. As the market moves, each individual stock is more or less affected. The extent of how the stock is affected by such general moves is measured by a Beta coefficient.
For example, If the beta of stock against S&P 500 is 2, then a 10% jump in the index return will cause a 20% jump in the stock return; the beta of 0.5 suggests that an asset is more stable than the market on average, i.e. stock return is expected to be half the market return and a 10% jump in index will cause only a 5% jump in the stock return.
Assets with high beta values are called aggressive, while assets with low beta values are called defensive. Aggressive assets are shares of companies, whose returns of which are extensively dependent on economic conditions. In general if the economy is on the rise, these companies tend to make large profits. For example, shares of automakers are aggressive. When investors expect the economy to grow, they choose aggressive assets. The shares of a company with returns that are weakly dependent on state of the market are defensive. For example utility companies' shares are defensive.
Beta is useful for asset analysis, for measuring sensitivity to the market, for designing portfolios with a desired risk level. The beta of stock against a market index (such as S&P 500 or DJX ) measures a stock's volatility relative to the market as a whole, i.e. shows how a stock's price movements relate to changes in the entire stock market. The greater the beta value, the more the market, or non-diversifiable, risk. Beta can be positive or negative. Positive beta value suggests that the market return and asset's return move in the same direction, when market conditions change. The overwhelming majority of assets have a positive beta. Assets with negative beta are an important instrument for portfolio diversification, because they allow one to create a portfolio with zero beta, i.e. without systematic risk. For example, if beta is -2, then a 10% up move in the market return will cause the stock return to drift down by 20%.
The beta and correlation can be solved for the following way:
Stock and index prices are observed on the fixed time interval. The following terms available for correlation and beta: 10, 20, 30, 60, 90, 120, 150, 180 days. The return of a stock can be calculated as the natural logarithm of the ratio of a stock's pric from the current day t to previous day t-1.
Thus, return \( x_t = \ln \frac{P_t}{P_{t-1}} \) where Pt is a close price on day t. Return of first stock is denoted \( x_{1}^{t} \) return of second stock is denoted \( x_{2}^{t} \)
\( \bar{S}_1 = \frac{1}{n} \displaystyle\sum_{t=1}^{n} x_1^t \)
\( \bar{S}_2 = \frac{1}{n} \displaystyle\sum_{t=1}^{n} x_2^t \)
\( HV^2_1 = \text{VAR}(S_1) = \frac{1}{n - 1} \displaystyle\sum_{t=1}^{n} (x_1^t - \bar{S}_1)^2 \)
\( HV^2_2 = \text{VAR}(S_2) = \frac{1}{n - 1} \displaystyle\sum_{t=1}^{n} (x_2^t - \bar{S}_2)^2 \)
\( \text{cov}(S_1, S_2) = \frac{1}{n-1} \displaystyle\sum (x_1^t - \bar{S}_1)(x_2^t- \bar{S}_2) \)
\( \text{corr}(S_1, S_2) = \frac{\text{cov}(S_1, S_2)}{\sqrt{\text{VAR}(S_1) * \text{VAR}(S_2)}} = \frac{\text{cov}(S_1, S_2)}{HV_1 * HV_2} \)
\( \text{Beta}(S_1, S_2) = \frac{\text{cov}(S_1, S_2)}{\text{VAR}(S_2)} = \text{corr}(S_1, S_2) * \frac{HV1}{HV2} \)
Note, correlation between implied volatilities of two assets can be calculated by the same formulas, using IV Index values instead of stock prices.
The correlation of two stock returns can be calculated as the covariance divided by their historical volatilities. Covariance is the tendency for two investment vehicles to exhibit similar price movements. Correlation values are expressed as percentages and range from -100% to +100%. The value (-100%) means that the returns are negatively correlated and that such assets entirely hedge each other when they move in opposite directions. Zero Correlation implies no correlation, which is good for diversification. The value (+100%) signifies that returns move in the same direction and the assets leverage each other. Note, 100% correlation between two assets does not mean that asset A should necessarily move by 1% in response to asset B moving up by 1% in the same direction. They could be correlated by 100% and asset B can move by 2% for every 1% move in asset A, if asset B has twice the volatility of asset A; Because correlation means the expected ratio of the moves between the assets divided by their corresponding volatilities.
When comparing the correlation and beta of stocks against major indexes (such as the S&P 500), attention should be paid to highly correlated stocks with large beta values.
Correlation Trading is one of the most popular approaches in the option markets. New strategies based on correlation are widely used, for example, the dispersion strategy.
For more information about dispersion trading , please read https://www.ivolatility.com/doc/Dispersion_Article.pdf
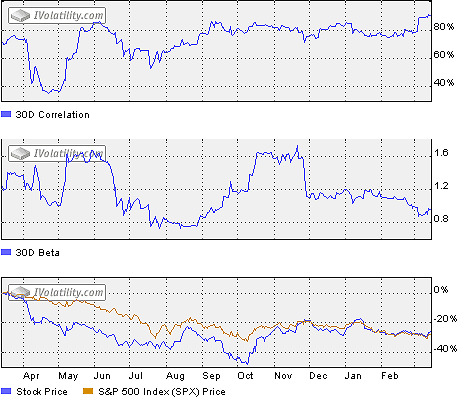
Example
The following chart shows the 30-day Correlation between IBM and SPX, 30-day Beta of IBM against SPX, and normalized IBM and SPX prices.